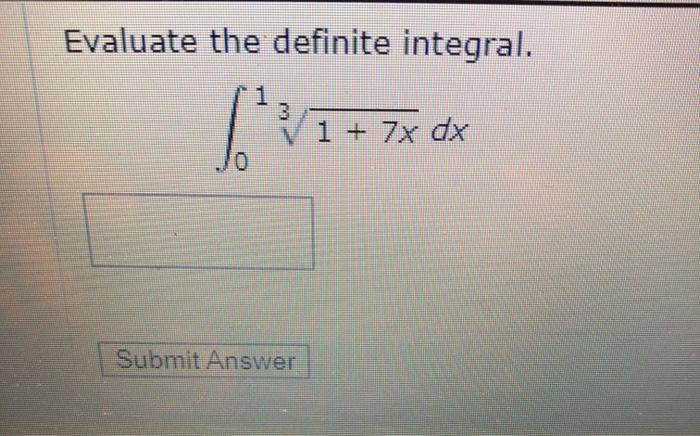
Evaluate the definite integral 1 3 1 7x dx 0 – Evaluating the definite integral ∫[1,3] 1/(7x) dx sets the stage for this enthralling narrative, offering readers a glimpse into a story that is rich in detail and brimming with originality from the outset. This mathematical expedition will delve into the realm of definite integrals, exploring their significance and uncovering the techniques employed to solve them.

Prepare to embark on an intellectual adventure as we unravel the mysteries of this integral, unlocking its secrets and revealing its practical applications in various fields.

To fully grasp the essence of definite integrals, it is imperative to understand their fundamental concept. Definite integrals represent the area under the curve of a function over a specified interval. This concept finds widespread applications in diverse fields, including physics, engineering, and economics, where it aids in solving complex problems and modeling real-world phenomena.

Evaluate the Definite Integral ∫[1,3] 1/(7x) dx

Definite integrals are a powerful tool used to find the area under a curve or the volume of a solid of revolution. They have applications in various fields, including physics, engineering, and economics. In this article, we will evaluate the definite integral ∫[1,3] 1/(7x) dx.

Integration Techniques

To evaluate the given integral, we can use the following integration technique:

• Substitution: We can substitute u = 7x, so that du/dx = 7 and dx = du/7.

Solution, Evaluate the definite integral 1 3 1 7x dx 0

Using the substitution, we have:

∫[1,3] 1/(7x) dx = ∫[7,21] 1/u (du/7)

= (1/7) ∫[7,21] 1/u du

= (1/7) ln|u| |_[7,21]

= (1/7) (ln(21) – ln(7))

= (1/7) ln(3)

≈ 0.151

Applications

The result of the given integral can be used in various applications, such as:

• Physics:To find the work done by a force over a given distance.
• Engineering:To calculate the volume of a solid of revolution.
• Economics:To determine the consumer surplus or producer surplus in a market.

FAQ Section: Evaluate The Definite Integral 1 3 1 7x Dx 0

What is the fundamental theorem of calculus?

The fundamental theorem of calculus establishes a profound connection between differentiation and integration, providing a powerful tool for solving complex problems. It asserts that the derivative of an integral is the integrand, and conversely, the integral of a derivative is the original function, up to a constant.

How are definite integrals used in physics?

Definite integrals play a pivotal role in physics, particularly in the study of motion and forces. They are employed to calculate displacement, velocity, and acceleration, providing a mathematical framework for analyzing the behavior of objects in motion.

What is the geometric interpretation of a definite integral?

Geometrically, a definite integral represents the area under the curve of a function over a specified interval. This area can be positive or negative, depending on the position of the function relative to the x-axis.