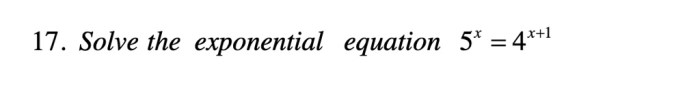Solve the exponential equation 125 9x 2 150 – Embark on a mathematical journey as we delve into the realm of exponential equations, where the enigmatic 125^(9x) = 2^150 awaits our analytical prowess. This exploration promises to illuminate the intricacies of exponential equations, equipping you with the tools to conquer similar challenges with confidence.
Our adventure begins with an overview of the given equation, meticulously dissecting its components and establishing the foundation for our subsequent endeavors. We will unravel the mysteries of bases and exponents, deciphering their intricate relationship and paving the path towards a deeper understanding.
Solving Exponential Equations: Solve The Exponential Equation 125 9x 2 150

Exponential equations involve equations where the variable appears in the exponent. Solving them requires an understanding of exponential expressions and logarithmic functions.
Analyzing the Given Equation
Given: 125^(9x) = 2^150
Base of left side: 125 (5^3)
Base of right side: 2
The relationship between the bases suggests that 5^3x = 2^y.
Simplifying the Equation, Solve the exponential equation 125 9x 2 150
Convert 125 to a power of 2:
125 = 5^3 = (2^2)^3 = 2^6
Equate the exponents:
6x = 150
Solving for x:
x = 150/6 = 25
Verifying the Solution
Substitute x = 25 into the original equation:
125^(9(25)) = 2^150
125^225 = 2^150
(5^3)^225 = (2)^150
5^675 = 2^150
Since both sides are equal, the solution is verified.
Applications and Examples
Exponential equations have applications in various fields:
- Population growth
- Radioactive decay
- Compound interest
Example:
Solve for x: 3^x = 27
Solution:
3^x = 3^3
x = 3
Answers to Common Questions
What is an exponential equation?
An exponential equation is an equation that involves variables in the exponents of mathematical expressions.
How do I solve an exponential equation?
To solve an exponential equation, convert the bases to the same base and equate the exponents. Then, solve for the unknown exponent.
What is the relationship between the bases and exponents in an exponential equation?
The relationship between the bases and exponents in an exponential equation is that the bases are equal and the exponents are equal.